Mixture of Experts
Mixture of experts (MoE) is a neural network architecture where separate linear models are trained for local regions in input dataset. These linear models are called experts and their outputs are combined with weights given by gating model. Gating model discriminates local regions in data and may employ different functions such as radial basis functions or simple dot product. If data present different characteristics for different regions of input space, one approach would be to run a clustering method on data as a preprocessing step and train separate models for each cluster. MoE architecture couples these clustering and separate model fitting tasks into a single task and may prove to be more successful on certain datasets. We can talk about two types of MoE architecture that differ in their clustering approaches. In competitive MoE, local regions in data are forced to focus on discrete sub-spaces in data while in cooperative type, there is no enforcement on location of regions and these regions may and most of the time will overlap.
First, I will present a formal definition of MoE architecture and update equations for training such a model. Afterwards, I will provide MoE implementation in MATLAB and illustrate it on a synthetic regression example.
\(X = \lbrace x, r \rbrace\) where \(x\) is a \(d\) x \(N\) matrix where each row vector contains input values and \(r\) is a \(K\) x \(N\) matrix where each row is a vector denoting which class a sample belongs to in classification problems or output values for each output dimension in case of regression.
\(j=1...D\) inputs, \(i=1...K\) outputs, \(h=1...H\) experts, \(\eta\) learning rate
Linear fit of expert h for output i: \(w_{ih} = v_{ih}^{T} x\)
Weight vector of each linear model: This vector is of size D+1 since we add a bias unit. \(v_{ih}\)
Local region center for expert h: \(m_h\) is a D-vector.
Gating Model, weight of expert h: Here dot product is used. \(g_h = \frac{ exp(m_h^T x) }{\Sigma_k exp(m_k^T x)}\)
Regression:
Output: \(y_i = \Sigma_{h=1}^{H} w_{ih} g_h\)
Classification:
Output: \(y_i\) are converted to posterior probabilities through softmax function. \(o_i = \frac{exp(y_i)}{\Sigma_k exp(y_k)}\)
Update equations for regression and classification are derived using gradient ascent. In regression, sum of squares of error is minimized where in classification likelihood of a training instance is maximized. When derived, update equations for regression and classification turn out to be same and given as follows for two types of MoE.
Cooperative MoE \(\Delta v_{ih} = \eta (r_i - o_i) g_h x\) \(\Delta m_h = \eta (r_i - o_i) (w_{ih} - y_i) g_h x\) ( \(o_i = y_i\) for regression )
Competitive MoE
\(\Delta v_{ih} = \eta f_h (r_i - y_{ih}) x\)
\(\Delta m_h = \eta (f_h - g_h) x\)
For classification, \(f_h = \frac{ g_h exp ( \Sigma_i r_i log y_{ih} )}{\Sigma_k g_k exp ( \Sigma_i r_i log y_{ik} )}\) \(y_{ih} = \frac{exp(w_{ih}}{\Sigma_k exp(w_{kh})}\)
For regression, \(f_h = \frac{ g_h exp ( 0.5 \Sigma_i (r_i - y_{ih})^2 )}{\Sigma_k g_k exp ( 0.5 \Sigma_i (r_i - y_{ik})^2 )}\) \(y_{ih} = w_{ih}\)
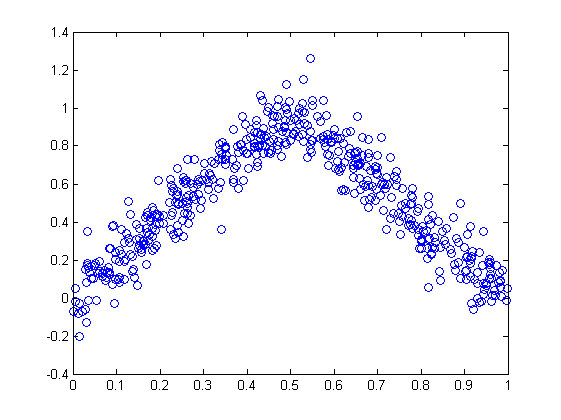
For testing my implementation I have generated synthetic regression and classification problems. Below can be seen plot of regression dataset. I have generated points from two linear models by using first linear model in first half of space and second model in the rest also adding some Gaussian noise to samples.
Two functions are implemented for realizing MoE architecture where first one TrainMixtureOfExperts is used to train model and TestMixtureOfExperts is utilized for testing instances on trained MoE network. Below code trains the network on training data and reports error for validation set.
1
2
3
4
5
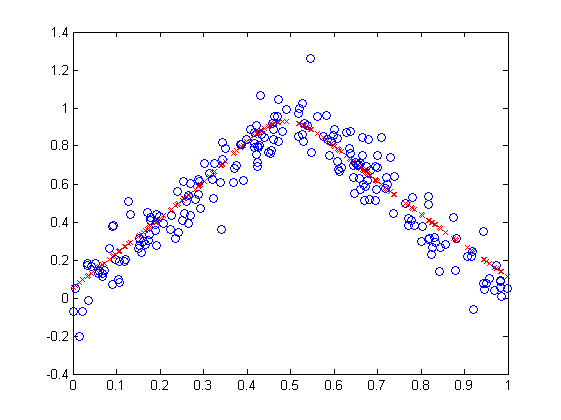
[v, m] = TrainMixtureOfExperts('regression', 'competitive', tx2, tr2, 2, 100, 0.5, 0.99);
[err, cr] = TestMixtureOfExperts('regression', vx2, vr2, v, m);
plot(vx2, cr, 'xr')
hold on
plot(vx2, vr2, 'ob')
It can also be seen in the below plot that MoE model learns the underlying model that generates quite successfully by analyzing the predicted outputs on given outputs visually.
All source code; MoE functions and synthetic data generation routines can be downloaded from here.